Слова де Бройна
Итак, что можно сказать про «наиболее плотные» слова для m и k, т.е. m-слова, содержащие в качестве своих подслов длины k все возможные m-слова длины k, причем ровно по одному разу каждое?
Такие слова или последовательности известны под именем слов или последовательностей де Бройна (de Bruijn) шага k. Они были известны для случая m = 2 еще в 1894 г.[5], а впоследствии были независимо переоткрыты де Бройном [6] и еще несколькими авторами [7, 8, 9]. В статье [6] де Бройн поставил и решил задачу о том, сколько имеется циклов длины mk (цикл — это класс эквивалентности слов по циклическим перестановкам их символов, например, 0110, 0011 и 1001 относятся к одному циклу), содержащих все возможные m-слова длины k. Полученный им ответ

Обзор [11] дает наиболее полный экскурс в теорию слов де Бройна и историю их использования для решения различных задач. Там они названы циклами нелинейных сдвиговых регистров полной длины (full length nonlinear shift register cycles). Среди задач, связанных с комбинаторикой слов, в которых возникают слова де Бройна можно отметить построение псевдослучайных последовательностей [12], построение кодов [13, 14], кодирование образов [15, 16], построение машин на основе сдвиговых регистров [11, 17, 18], организацию CDMA-сетей. В связи с тестированием программного обеспечения они упоминаются в [19].
Слова де Бройна связаны с графами специального вида, называемыми также графами де Бройна. Граф де Бройна с параметрами m?1 и k?1 B(m, k) — это ориентированный граф с mk-1 вершинами V(m, k) = [0..(m-1)]k-1, являющимися всеми возможными m-словами длины (k-1), и ребрами E(m, k) = [0..(m-1)]k, являющимися всеми возможными m-словами длины k.
При этом ребро x1x2…xk-1xk начинается в вершине x1x2…xk-1
и заканчивается в вершине x2…xk-1xk. Примеры графов де Бройна изображены на рис. 1. Достаточно легко убедиться в выполнении следующего утверждения. Утверждение 1.
1) Граф B(m, 1) имеет ровно одну вершину — пустое слово — и m ребер-петель. 2) Граф B(m, 2)
изоморфен полному ориентированному графу с петлями на m вершинах. 3) Количества входящих и выходящих ребер для любой вершины B(m, k) равны m. "v Î V(m, k) in-deg(v) = out-deg(v) = m
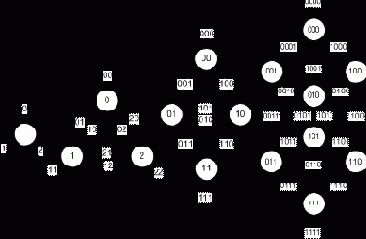
Рисунок 1. Графы B(3, 1), B(3, 2), B(2, 3), B(2, 4). Последний пункт непосредственно влечет следующее. Утверждение 2. 1) Для всех m, k ? 1 граф B(m, k) эйлеров, т.е. в нем существует цикл, включающий все ребра 2) Любой эйлеров путь в B(m, k) однозначно соответствует слову де Бройна, а значит такие слова существуют для всех m, k ? 1.
Для построения слова, соответствующего пути в B(m, k), выпишем слово, соответствующее первому ребру пути, затем для каждого следующего ребра пути будем приписывать в конец полученного слова последний символ этого ребра. Определим для ориентированного графа G дуальный граф L(G) как граф, имеющий в качестве вершин множество ребер G, а в качестве ребер — множество пар смежных ребер G, т.е. таких, что конец первой является началом второй. При этом ребро L(G) начинается в вершине, соответствующей первому элементу пары, а кончается в вершине, соответствующей второму. Утверждение 3. 1) Для всех m, k ? 1 дуальный граф к B(m, k) изоморфен B(m, k+1).
Это легко проверить, заметив, что паре смежных ребер B(m, k) соответсвует слово длины (k+1), построенное по правилу из второго пункта предыдущего замечания.
Кроме того, все m-слова длины (k+1) могут быть получены таким способом. 2) Эйлеров путь или цикл на графе G соответствует гамильтонову (проходящему через каждую вершину ровно один раз) пути или циклу на графе L(G) 3) Для всех m, k ? 1 граф B(m, k) имеет гамильтонов цикл Сделанные замечания позволяют определить достаточно эффективный алгоритм построения слов де Бройна — для этого достаточно построить граф B(m, k), что требует объема памяти и времени O(mk), и найти в нем эйлеров цикл, что можно сделать за время, пропорциональное количеству ребер графа, т.е.
опять за O(mk), и используя такой же объем памяти. Длина слова де Бройна равна mk+k-1, т.е. тоже O(mk), следовательно, такой алгоритм оптимален по порядку. Можно улучшить «внутренние» показатели эффективности такого алгоритма, т.е. уменьшить объем памяти, занимаемый внутренними структурами данных и время их обработки, не учитывая внешнюю память и время, используемые для вывода результата. Различные алгоритмы для порождения слов де Бройна довольно часто упоминаются в литературе, в том числе и алгоритмы с лучшими показателями «внутренней» эффективности. Часть из них основана на неожиданной связи между словами де Бройна и словами Линдона (Lyndon words). Слово Линдона длины k в алфавите мощности m — это лексикографически минимальный представитель m-цикла, т.е. класса эквивалентности m-слов по циклическим перестановкам их символов. Оказывается, что верно следующее утверждение. Утверждение 4. [11] Конкатенация лексикографически упорядоченной последовательности всех слов Линдона длин, делящих k, в некотором алфавите дает лексикографически минимальный цикл де Бройна шага k в том же алфавите (для получения из него слова де Бройна достаточно добавить первые k-1 символов из начала в конец). Эффективный (требующий ограниченного константой «внутреннего» времени на построение одного слова Линдона) алгоритм построения слов Линдона и слов де Бройна на их основе представлен в [20]. Другие алгоритмы можно найти в [21–28]. В работе [29] эмпирически сравнивается эффективность по времени алгоритмов из [20], [25] и [27], и последний демонстрирует наиболее высокое быстродействие.
