Обобщенное состояние
Используется целочисленное или натуральное состояние 0, 1, 2, … . Функция вычисления обобщенного состояния возвращает количество элементов списка. Для обеспечения конечности обобщенных состояний вводится ограничение на количество состояний, задаваемое как параметр сценария.
Используется целочисленное или натуральное состояние 0, 1, 2, … . Функция вычисления обобщенного состояния возвращает количество элементов множества. Для обеспечения конечности обобщенных состояний вводится параметр сценария, который может задавать ограничение как на количество состояний, так и на количество разнообразных элементов, итерируемых в сценарных методах.
Тип состояния зависит от типов элементов произведения. В общем случае можно пользоваться PairComplexGenState и ListComplexGenState, конструируемыми из пары и списка обобщенных состояний соответственно. Для произведения целочисленных состояний можно пользоваться классами обобщенных состояний IntPairGenState, IntTripleGenState, IntListGenState.
В качестве обобщенного состояния выбирается мультимножество, элементы которого - количество непосредственных дочерних вершин. Рассмотрим пример.
На рис. 7 показаны два дерева, в которых одна вершина имеет две дочерних, одна имеет одну дочернюю, и две вершины в каждом дереве не имеют дочерних вершин. Таким образом, обоим этим деревьям соответствует одно и тоже обобщенное состояние, мультимножество {0,0,1,2}.
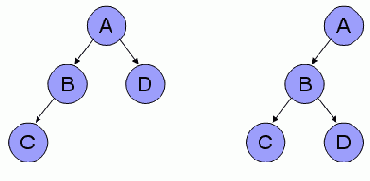
Рис. 7. Примеры деревьев
Результаты подсчета количества обобщенных состояний в зависимости от числа вершин приведены в таблице 2. Как видно, количество обобщенных состояний значительно меньше числа корневых деревьев для того же числа вершин. Это делает данное обобщенное состояние практически пригодным для использования при тестировании.
| Число корневых деревьев | 1 | 9 | 719 | 87811 | 12826228 | 2067174645 |
| Число обобщенных состояний | 1 | 5 | 30 | 135 | 490 | 1575 |
Таблица 2. Количество обобщенных состояний
Вместе с тем, данное обобщенное состояние определяет разнообразные виды деревьев. Мультимножества вида {0, …, 0, N}, где N - количество вершин определяют широкие деревья, а мультимножества вида {0, 1, …, 1} определяют высокие деревья.
